原文題目

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

題目摘要

1. 題目給予一個m*n的矩陣，每一列數字皆按升序排列，並且每一列最後一行數字皆小於下一列第一行數字（即為Z字形排序）。
2. 題目所求：判斷target是否存在於此矩陣中，回傳True/False。

Example 1:

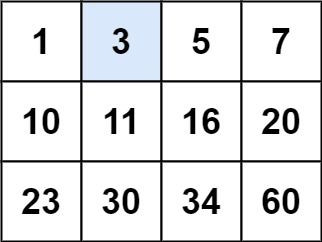
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

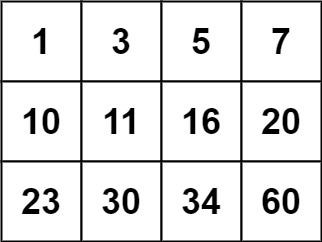
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

解題思路一

1. 矩陣轉換：
   • 將二維矩陣視為一個一維陣列。假設矩陣的列數為 m，行數為 n。這樣，矩陣中的每個位置 matrix[x,y] 可以表示一維陣列中的索引 ，並可透過除法所得之商數和餘數找出矩陣對應(x,y)位置的值。
2. 設定左右指標：
   • 設定left和right指標分別為陣列第一位和最後一位。
3. 找到中間點：
   • 我們在給定的陣列中找出中間點的元素 mid。
4. 比較和更新範圍：
   • 如果矩陣中的值等於目標值，則返回 true。如果矩陣中的值小於目標值，則將左指標移到 mid + 1。如果矩陣中的值大於目標值，則將右指標移到 mid - 1。
5. 結束條件：
   • 當左指標大於右指標時，表示目標值不在矩陣中，此時返回 false。

程式碼一

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length; //設立m為矩陣列數
        int n = matrix[0].length; //設立n為矩陣第一列之行數，即矩陣行數
        int left = 0; //設立左指標為陣列第一位，索引值為0
        int right = m * n - 1; //設立右指標為陣列最後一位，索引值為矩陣個數(m*n)-1
        while( left <= right ){
            int mid = ( left + right ) / 2; //設定中間值
            int x = mid / n; //設立x為mid列數（商數）
            int y = mid % n; //設立y為mid行數（餘數）
            //若mid所指向之矩陣值（中間值）即為target則回傳True
            if( matrix[x][y] == target){
	            return true;
            }
            else if ( matrix[x][y] < target){ //當中間值小於目標值
                left = mid + 1; //將範圍限制在中間值後一位（新左指標）與右指標
            }
            else { //當中間值大於目標值
	            right = mid - 1; //將範圍限制在左指標與中間值前一位（新右指標）
            }
        }
        return false; //若目標值不在矩陣中則回傳False
    }
}

解題思路二

1. 尋找可能包含目標值的列：
   • 首先，你需要找到矩陣中可能包含目標值的列。由於每一列的數值都是按升序排列的，你可以利用二分搜尋來定位目標值可能所在的列。
   • 使用 firstRow 和 lastRow 來表示矩陣的列範圍（第一列至最後一列），通過比較中間列的第一個元素和最後一個元素來判斷目標值是否位於該列。如果目標值在該列的範圍內，則這一列可能包含目標值；如果不在這個範圍內，就根據目標值大小調整行範圍。
2. 確認目標值是否在找到的列中：
   • 在確定了目標值可能在的列後，接著需要在該列中使用二分搜尋來查找目標值。
   • 設定 firstColumn 和 lastColumn 來表示目標列的行範圍（第一行至最後一行）。通過比較中間行的值來檢查目標值是否與之相等，或者調整行範圍。
3. 返回結果：
   • 如果在行或列中找到目標值，則返回 true；如果在所有可能的行和列中都未找到目標值，則返回 false。

程式碼二

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int firstRow = 0; //設立第一列指標為陣列第一列，索引值為0
        int lastRow = matrix.length - 1; //設立最後列指標為陣列最後一列，索引值為矩陣列數-1
        //判斷目標值可能包含在矩陣的第幾列
        while (firstRow <= lastRow) {
            int midRow = (firstRow + lastRow) / 2; //設立中間列
            //當中間列可能包含target，則跳出迴圈繼續判斷是否有出現
            if (matrix[midRow][0] <= target && target <= matrix[midRow][matrix[0].length-1]) {
                break;
            }
            //當target小於中間列第一位數，則將範圍限制在第一列指標與中間列的前一列（新最後列指標）
            else if (matrix[midRow][0] > target){
                lastRow = midRow - 1;
            }
            //當target大於中間列最後一位數，則將範圍限制在中間列的後一列(新第一列指標)與最後列指標
            else{
                firstRow = midRow +1;
            }
        }
        int row = (firstRow + lastRow) / 2; //設立可能包含target的列
        int firstColumn = 0; //設立第一行指標為目標列的第一行，索引值為0
        int lastColumn = matrix[row].length - 1; //設立最後行指標為目標列的最後一行，索引值為矩陣row列的長度-1
        
        //判斷目標值是否出現在矩陣row列的第幾行
        while (firstColumn <= lastColumn){
            int midColumn = (firstColumn + lastColumn) / 2; //設立中間行
            //當row列中間行值等於target，代表矩陣有target，則跳出迴圈回傳true
            if (matrix[row][midColumn] == target){
                return true;
            }
            //當row列中間行值大於target，則將範圍限制在第一行指標與中間行的前一行(新最後行指標)
            else if (matrix[row][midColumn] > target){
                lastColumn = midColumn - 1;
            }
            //當row列中間行值小於target，則將範圍限制在中間行的後一行(新第一行指標)與最後行指標
            else{
                firstColumn = midColumn +1;
            }
        }  
        return false; //如果row列沒有一行等於target，代表矩陣沒有target，則回傳false

結論

想像你在一個大型超市找尋某個特定的商品。首先，你會先查看超市的走道標示來確定該商品的分類區域（這就像是確定目標值所在的列）。一旦確定了分區，你接下來就會在該類型走道的貨架上尋找具體的商品（這相當於在確定的列內進行二分搜尋）。透過這種分步驟的方法，你能夠快速找到目標商品，避免了在整個超市中隨意搜尋的麻煩。這就是如何利用排序和分區來提高搜尋效率的實際應用。